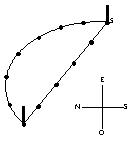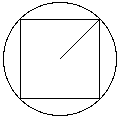
1) Un callejón sin salida
Al parecer, el primer matemático que abordó el problema fue Hipócrates de Quio, contemporáneo de Sócrates (y que no debe ser confundido con Hipócrates de Cos, el gran médico y fisiólogo), quien mediante un método sumamente ingenioso demostró la posibilidad de construir un cuadrado de superficie exactamente igual a la de una lúnula, es decir, una figura comprendida entre dos arcos de circunferencias distintas. Un par de siglos después, Arquímedes de Siracusa llegó más lejos, cuadrando un segmento parabólico, o sea una figura plana comprendida entre un arco de parábola y una línea recta. Pero nadie ha logrado cuadrar un círculo mediante procedimientos geométricos, y hace ya mucho tiempo que el problema fue dejado de lado por considerárselo una quimera. Y efectivamente se trata de una quimera si por "cuadratura del círculo" ha de entenderse, como por lo común se ha entendido desde Hipócrates hasta el presente, el establecimiento de una equivalencia cuantitativa, o sea un círculo y un cuadrado de áreas iguales.

"El cambio del círculo en un cuadrado equivalente, (es decir de igual superficie si uno se coloca desde el punto de vista cuantitativo, pero esto no es sino una expresión totalmente exterior de lo que se trata en realidad), es lo que se designa como la 'cuadratura del círculo'; quienes declaran que éste es un problema insoluble, aún cuando ignoran totalmente su significación profunda, tienen no obstante razón de hecho, puesto que esta 'cuadratura', entendida en su verdadero sentido, no podrá ser realizada sino al final mismo del ciclo.¹⁷ Desde este punto de vista, la imposibilidad de resolver la "cuadratura del círculo" bien puede ser considerada como un símbolo de que "nadie conoce el día ni la hora": Nadie sabe cuándo arribará el fin de su ciclo, ya se trate de su existencia individual o de la existencia de su mundo, y, en consecuencia, dada la necesaria correspondencia analógica entre todos los grados de la Existencia universal, nadie puede obtener a partir de un círculo un cuadrado equivalente.

Ahora bien: Si dejamos de considerar al ciclo en sí mismo, es decir en forma aislada, y pasamos a considerarlo como eslabón de una cadena, veremos que no hay razón alguna que obligue a suponer que el cuadrado y el círculo de que se trata deban ser necesariamente equivalentes en lo que respecta a sus áreas. Por el contrario, hay suficientes razones para afirmar que la Jerusalem celeste no puede ni debe guardar ninguna equivalencia cuantitativa con el Paraíso terrestre:

"Podría decirse que es este mismo círculo el que se cambia finalmente en un cuadrado, puesto que los dos extremos deben reunirse o, más bien (dado que el ciclo nunca es realmente cerrado, lo que implicaría una repetición imposible), corresponderse exactamente".¹⁸

Si el área del cuadrado fuese igual a la del círculo, si la "cuadratura del círculo" diese por resultado áreas iguales, también debería obtenerse el mismo resultado luego de la "circulatura del cuadrado", con lo cual el nuevo Paraíso terrestre sería idéntico al Paraíso terrestre del ciclo anterior. En tal caso, nos hallaríamos ante el famoso "mito del eterno retorno" que, como se sabe, fue una invención de Nietszche desprovista de todo fundamento tradicional.

"Es evidente que las épocas del tiempo están cualitativamente diferenciadas por los acontecimientos que en ellas se desarrollan, así como las porciones del espacio lo están por los cuerpos que ellas contienen, y que no se puede de manera alguna considerar como realmente equivalentes a las duraciones cuantitativamente iguales pero colmadas por series de acontecimientos completamente diferentes; también es de observación corriente que la igualdad cuantitativa, en la apreciación mental de la duración, desaparece completamente delante de la diferencia cualitativa".¹⁹

Por otra parte, "la tendencia a la uniformidad, que se aplica en el dominio 'natural' tanto como en el dominio humano, conduce a admitir, y aún a colocar en cierto modo como principio (deberíamos decir más bien como 'pseudoprincipio'), que hay repetición de fenómenos idénticos lo cual, en virtud del 'principio de los indiscernibles', no es en realidad más que una imposibilidad pura y simple. Esta idea se traduce notablemente en la afirmación corriente de que 'las mismas causas producen siempre los mismos efectos', lo cual, enunciado de esta forma, es propiamente absurdo, puesto que, de hecho, jamás podría haber ni las mismas causas ni los mismos efectos en un orden sucesivo de manifestación; ¿y no se llega hasta decir comúnmente que 'la historia se repite', en tanto que la verdad es que solamente hay correspondencias analógicas entre ciertos períodos y entre ciertos acontecimientos? Lo que habría que decir es que causas comparables bajo ciertas relaciones producen efectos igualmente comparables bajo las mismas relaciones; pero, dejando de lado las semejanzas que son, si se quiere, como una identidad parcial, siempre y necesariamente hay diferencias, por el hecho mismo de que, por hipótesis, se trata de dos cosas distintas y no de una sola y misma cosa".²⁰

La imposibilidad de equivalencia cuantitativa entre el cuadrado y su círculo de origen, no está determinada, pues, por consideraciones de orden geométrico sino por una cuestión de principios. En todo caso, podríamos decir que la imposibilidad geométrica es un símbolo de la "imposibilidad principial", si se nos permite la expresión. Este es el verdadero motivo por el cual, a lo largo de veinticinco siglos, todos los intentos por resolver el problema de la "cuadratura del círculo" desembocaron en un callejón sin salida.

Si bien se mira, los resultados obtenidos por Hipócrates de Quio y por Arquímedes de Siracusa, sin menoscabo del ingenio y aún del genio que éstos revelan, lejos de constituir "pasos adelante", constituyeron verdaderos "pasos hacia atrás": A medida que los matemáticos creían avanzar hacia la resolución cuantitativa del problema, lo que en realidad hacían era alejarse cada vez más de los principios que dan al problema su razón de ser. No es de extrañar, entonces, que lo que había comenzado como una seria y metódica búsqueda (también una quimera puede ser buscada de manera seria y metódica), terminase por degenerar, con el correr de los siglos, en una pseudo-numerología con pretensiones "mágicas", "mánticas" y "ocultistas" de la peor especie.

¿Qué hacer cuando uno se encuentra en un callejón sin salida?: Salir por la entrada.

2) Los términos de comparación
"Salir por la entrada" significa, en este caso, renunciar a toda búsqueda de equivalencias cuantitativas y plantear el problema en otros términos: ¿Cuál es la proporción que un círculo y un cuadrado deben guardar entre sí para que la relación entre ambas figuras pueda ser considerada como un símbolo del fin de un ciclo de manifestación? Es evidente que, si se trata de una proporción, da exactamente lo mismo considerar las áreas, los perímetros o cualquier otro "factor cuantitativo" mediante el cual puedan ser comparados el círculo y su correspondiente cuadrado. No obstante, es preciso escoger alguno de entre todos los posibles términos de comparación. ¿Qué criterio de elección habremos de adoptar?

Tanto el área como el perímetro de un círculo dependen absolutamente de su radio, en tanto que éste sólo depende del centro, del principio que le ha dado origen. Cabe pues escoger al radio por ser éste el "más principial" de cuantos posibles términos de comparación podrían hallarse en un círculo. (Desde luego, el centro mismo no podría ser tomado como término de comparación ya que su "valor", así en el círculo como en el cuadrado -como también en cualquier otra figura o cosa-, será siempre e invariablemente 1 cuando esté manifiesto, y 0 cuando no lo esté).

Ahora bien: ¿Cuál de los elementos que conforman un cuadrado puede ser considerado análogo al radio de un círculo? A primera vista, son dos los elementos a considerar: la semi-diagonal y la apotema. Ambas parten del centro y llegan hasta los extremos del cuadrado: la semi-diagonal llega hasta un vértice y la apotema llega hasta el punto medio de un lado; y tanto el área como el perímetro del cuadrado dependen mediata y absolutamente a la vez de la apotema y de la semi-diagonal, mientras que éstas sólo dependen del centro. Por lo demás, un cuadrado puede ser considerado como la resultante del giro de la cruz que conforman tanto sus diagonales como sus apotemas. ¿Es entonces indistinto elegir la apotema o la semi-diagonal como términos de comparación con el radio del círculo? No, porque nada en el universo manifiesto es "indistinto".

"Cabe aquí hacer mención a lo que Leibnitz denominó el 'principio de los indiscernibles', en virtud del cual en ninguna parte pueden existir dos seres idénticos, es decir semejantes en todas las relaciones entre ellos; es ésta (…) una consecuencia inmediata de la ilimitación de la posibilidad universal, que entraña la ausencia de toda repetición en las posibilidades particulares; y se puede decir todavía que dos seres a los que se supone idénticos no serían verdaderamente dos, sino que, coincidiendo en todo, no serían en realidad sino uno solo; pero precisamente, para que los seres no sean idénticos o indiscernibles, es preciso que haya siempre entre ellos alguna diferencia cualitativa, por lo tanto, que sus determinaciones no sean jamás puramente cuantitativas".²¹ En nuestro caso, tratándose de elementos que evidentemente no son idénticos, con mayor razón aún habremos de indagar en sus diferencias cualitativas.

Cuando conocemos la medida de la apotema de un cuadrado, también podemos conocer la medida de sus lados (ya que cada lado mide el doble de la apotema), y, en consecuencia, también su área y su perímetro. Pero en tal caso, la diagonal del cuadrado (y la semi-diagonal, obviamente) resultará inconmensurable ya que, como es sabido, d = 1 x Ö2, siendo Ö2 un número inconmensurable. Esta es, en el caso que nos ocupa, la diferencia cualitativa entre la apotema y la semi-diagonal: La primera es mensurable mientras que la segunda no lo es.

Podría objetarse que, en el caso de que se conociese la medida de la semi-diagonal, serían la apotema, los lados, el perímetro y el área del cuadrado los inconmensurables, con lo cual la diferencia cualitativa que hemos mencionado resultaría "reversible". Esto es cierto desde un punto de vista meramente cuantitativo: 1 = d ÷ Ö2. Pero desde otro punto de vista, no hay reversibilidad posible. En efecto, siendo el cuadrado un símbolo del acabamiento del ciclo, de la fijación, de la detención del tiempo y de su "transmutación en espacio", salta a la vista su naturaleza espacial, finita, definida y, por lo tanto, necesariamente mensurable; y esta es la razón por la cual podemos decir que la apotema está "más cerca" de la naturaleza del cuadrado que la semi-diagonal, toda vez que ésta, o bien es inconmensurable, o bien es un "factor de inconmensurabilidad". En consecuencia, hemos de considerar, en este caso, a la apotema como el elemento que, en el cuadrado, es análogo al radio del círculo.²²

La figura que, por lo general, se toma como representativa de la "cuadratura del círculo" es la de un cuadrado inscripto en una circunferencia:

Esta figura es perfectamente coherente como símbolo, y lo es en más de un sentido. Por ejemplo, el radio del círculo es aquí idéntico a la semi-diagonal del cuadrado, quedando así claramente simbolizado que el círculo y el cuadrado, es decir, el Cielo y la Tierra, comparten el mismo "principio dinámico", por cuanto el círculo proviene del giro de su radio y el cuadrado proviene del giro de la cruz formada por sus diagonales. Sin embargo, nosotros estamos ahora considerando un círculo y un cuadrado que no simbolizan al Cielo y a la Tierra "en general", sino al Paraíso terrestre y a la Jerusalem celeste en particular, es decir, al comienzo y al fin de un ciclo de manifestación; y la figura del cuadrado inscripto en el círculo es insuficiente para sugerir esta idea. Recordemos, además, que en el Apocalipsis (XXI, 16) está expresamente indicada la medida de cada lado de la Jerusalem celeste: ". y él midió la ciudad con la caña, doce mil estadios: la largura y la anchura y la altura de ella son iguales". Y puesto que se conoce el lado, también se conoce la apotema, mas no la semi-diagonal.

Tenemos así los dos "términos de comparación": el radio y la apotema; pero, ¿qué radio y qué apotema? ¿Cuáles deben ser sus medidas o, mejor dicho, cuál debe ser la proporción en que mutuamente se vinculan? ¿Y cuál ha de ser el "elemento vinculante"? Además, no se trata aquí de vincular un radio y una apotema existentes por sí mismos, independientes el uno de la otra, sino un círculo que deviene cuadrado y un radio que deviene apotema, de modo que la proporción entre ambos estará determinada, necesariamente, por la ley que rige ese devenir. El Paraíso terrestre deviene la Jerusalem celeste a fin de que se cumpla la ley de formación y destrucción del mundo que se considera, la cual, a su vez, es una modalidad particular de la Ley universal. Un ciclo particular de manifestación reproduce "a escala" el ciclo total de la Manifestación y, por lo tanto, en su propia medida, re-crea y garantiza el Orden del Mundo. Desde este punto de vista, el "pasaje" del Paraíso terrestre a la Jerusalem celeste es, propiamente, un acto ritual. Consecuentemente, y analógicamente, la transformación del círculo en cuadrado y del radio en apotema, ha de ser también un acto ritual; y sólo en tanto que así sea, la figura que resulte merecerá ser considerada un símbolo, toda vez que un símbolo no es sino la "fijación" de un rito.

3) Una construcción tradicional

Entre los aymaras de Bolivia y del Perú, el modo tradicional de trazar la planta de una vivienda es el siguiente:

- Se toma una cuerda lo suficientemente larga y se la divide en doce partes iguales mediante la confección de once nudos:

- Se ata el primer extremo de la cuerda a una estaca; se extiende la cuerda en dirección Noroeste-Sureste, y, a la altura del 5º nudo, se clava a tierra una segunda estaca, enlazándola con este 5º nudo. Luego, se ata el extremo suelto de la cuerda a la primera estaca:

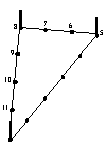
- Se toma la cuerda por su 8º nudo y se la tensa todo lo que resulte posible en dirección al Noreste. Allí donde ha quedado el 8º nudo, se clava a tierra una tercera estaca:

Como bien puede apreciarse, ha quedado conformado un triángulo rectángulo cuyos lados guardan entre sí la exacta proporción del "triángulo pitagórico": 3, 4, 5. Y esto ha sido logrado sin necesidad de efectuar ninguna medición.

- Ahora se suelta la cuerda de la tercera estaca y se la toma por el 9º nudo. Se la hace pasar por sobre la "hipotenusa", se la tensa hasta donde resulte posible en dirección Suroeste y, allí donde ha quedado el 9º nudo, se clava a tierra la cuarta y última estaca:

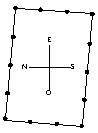
De este modo ha quedado determinada una planta rectangular de 3 x 4 (aquí no interesa la unidad de medida utilizada sino la proporción obtenida), cuyos lados están casi perfectamente orientados en dirección a los cuatro puntos cardinales (si la "hipotenusa" ha sido trazada en exacta dirección NO-SE, la desviación de la planta respecto a los puntos cardinales será inferior a los 5°, lo cual es prácticamente insignificante):

En base a esta planta se edificará la vivienda, reemplazándose las estacas por cuatro postes que simbolizan los cuatro pilares que sostienen el Cielo sobre la Tierra.

Dijimos que los doce tramos de la cuerda se determinan mediante once nudos, pero si tenemos en cuenta que los dos extremos de la cuerda se atan al primer poste (que es aquí "el alfa y el omega" de todo el trazado), resulta que los nudos son, en realidad, doce, toda vez que la primera atadura y la última deben ser consideradas como una sola, dada la analogía entre el principio y el final de todo ciclo de manifestación y, por lo tanto, de todo procedimiento realizado conforme al orden natural.

Esta cuerda con doce nudos guarda una evidente similitud con la "cadena de unión" que rodea la parte superior de la Logia masónica.

"Para comprender de qué se trata, es preciso ante todo recordar que, desde el punto de vista tradicional, todo edificio, cualquiera que fuere, se construía siempre según un modelo cósmico; por otra parte, se especifica expresamente que la Logia es una imagen del cosmos, y sin duda es éste el último recuerdo que de aquello ha subsistido hasta hoy en el mundo occidental. Siendo así, el emplazamiento de un edificio debía ser determinado y 'encuadrado' por algo que correspondiera de algún modo a lo que podría llamarse el 'marco' mismo del cosmos (…), y podemos decir ya que el trazado 'materializado' por el cordel representaba, propiamente hablando, su proyección terrestre. (…)

"Lo que hace particularmente neto el sentido del simbolismo es esto: mientras que el cordel, en cuanto instrumento, es, naturalmente, una simple línea, la 'cadena de unión' al contrario, tiene nudos de trecho en trecho; estos nudos son, o deben ser normalmente, en número de doce, y corresponden así, evidentemente, a los signos del Zodíaco. En efecto, el Zodíaco, en el interior del cual se mueven los planetas, constituye verdaderamente la 'envoltura' del cosmos.".²³

La planta de la Logia masónica es un rectángulo en proporción 2:1, o sea que sus lados mayores miden el doble que los menores, en tanto que, como vimos, la planta de la vivienda aymara es un rectángulo en proporción 3:4. Por otra parte, el tendido de la cuerda aymara es diferente al de la "cadena de unión" ya que, en este caso, sus extremos no se juntan y quedan ambos orientados hacia Occidente. Pero no obstante estas diferencias, que reflejan puntos de vista diferentes -pero no contrapuestos- respecto a un mismo simbolismo, lo importante es destacar que, "tradicionalmente, todo edificio está construido según un modelo cósmico; mientras no existió la distinción entre 'sagrado' y 'profano' es decir, mientras el punto de vista profano no había surgido aún por efectos de un debilitamiento de la tradición, siempre y en todas partes fue así, inclusive para las casas particulares. La casa era entonces una imagen del cosmos, es decir, como un 'pequeño mundo' cerrado y completo en sí.".²⁴

Guénon se expresa en tiempo pasado pues se dirige al lector occidental, y es precisamente en Occidente donde la tradición se ha debilitado hasta casi extinguirse y donde el punto de vista profano llegó a penetrar todos los aspectos de la vida social, incluyendo -y no en poca medida- el aspecto religioso, de modo que las construcciones tradicionales pertenecen realmente al pasado (hace siglos que se construyen iglesias orientadas hacia cualquier parte, menos hacia donde corresponde). Pero va de suyo que el "mundo occidental" al que se refiere Guénon no incluye al pueblo aymara, ni a los demás pueblos tradicionales -"indígenas"- de América, ninguno de los cuales pertenece, desde ningún punto de vista, a la civilización occidental, sea cual fuere el grado de "aculturación" a que Occidente los haya transitoriamente sometido en nombre del "progreso", de la "democracia" o de la "religión verdadera". Las mismas palabras que Guénon dedicara a la actual relación entre Occidente y los pueblos orientales, son rigurosamente aplicables, término a término, a la relación entre Occidente y los pueblos tradicionales americanos²⁵:

"Cuando la resistencia a una invasión extranjera es el hecho de un pueblo occidental, ella se llama 'patriotismo' y es digna de todos los elogios; cuando ella es el hecho de un pueblo oriental, se llama 'fanatismo' o 'xenofobia' y no amerita más que el odio o el desprecio. Por lo demás, ¿no es acaso en nombre del 'Derecho', de la 'Libertad', de la 'Justicia' y de la 'Civilización' que los Europeos pretenden imponer por todas partes su dominación, y prohibir a todo hombre vivir y pensar de otro modo al que ellos mismos viven y piensan? (…) En todo caso, lo que hay aquí de cierto es que los Orientales no amenazan a nadie ni sueñan siquiera con invadir Occidente de un modo o de otro; ellos tienen, por el momento, bastante que hacer defendiéndose contra la opresión europea, que amenaza alcanzarlos hasta en su espíritu; y es cuanto menos curioso el ver a los agresores colocándose en víctimas.

"Era necesaria esta aclaración, pues hay ciertas cosas que deben ser dichas".²⁶